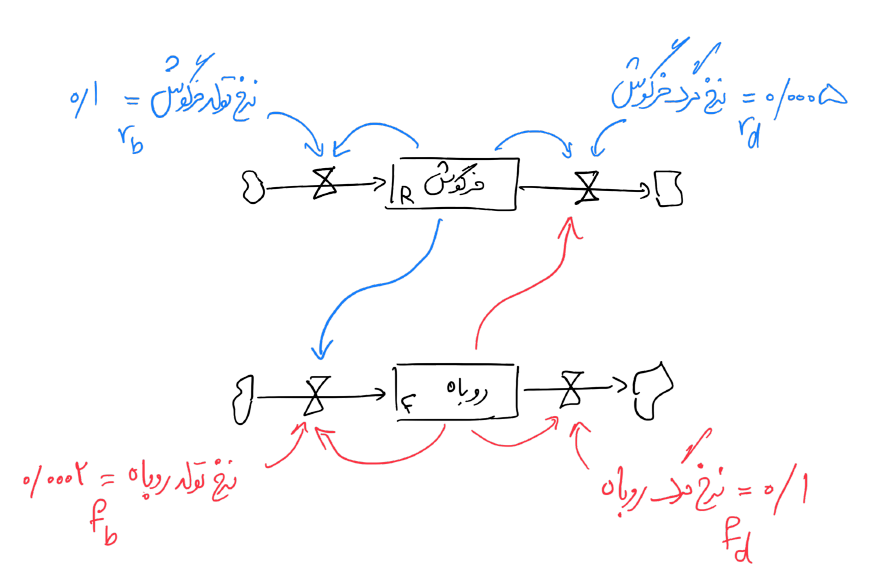
شبیهسازی دینامیکی سیستم از آوردههای نگرش سیستمی در حل مسأله است. این گونه از شبیهسازی بالا به پایین1، با اتصال متغیرهای حالت و تعیین روابط بازگشتی بین آنها، مدلی از واقعیت میسازد. مثلاً با بررسی روابط بین روباهها و خرگوشها، مدل دینامیکی زیر از جمعیت آنها به دست میآید.
 |
|---|
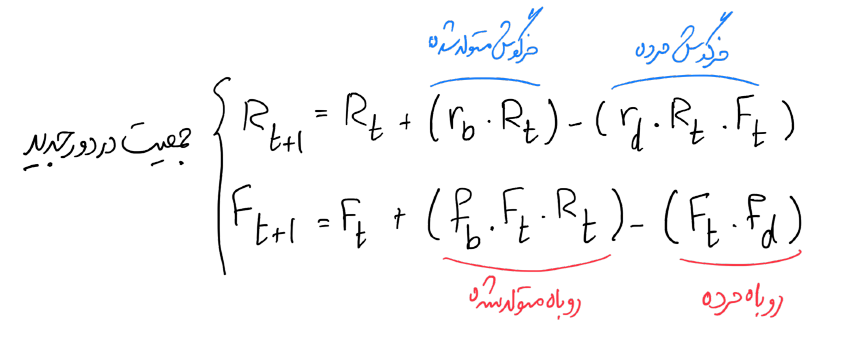 |
|---|
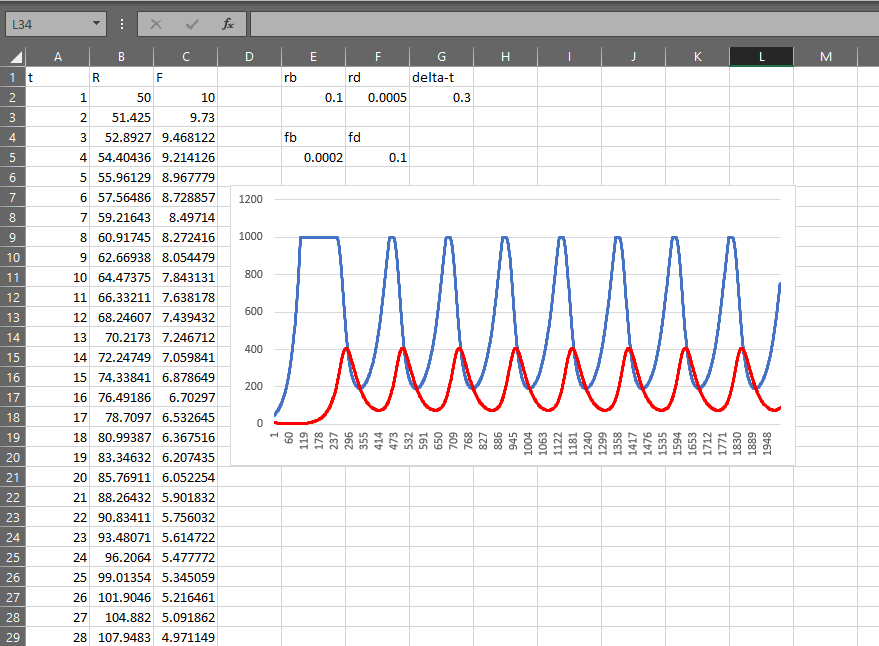
شبیهسازی این روابط، زمانی اتفاق میافتد که متغیر زمانی t را معرفی کنیم و جمعیت را به ازای مقادیر مختلف t محاسبه کنیم. این کار به سادگی در نرمافزار اکسل قابل پیادهسازی است2.
 |
|---|
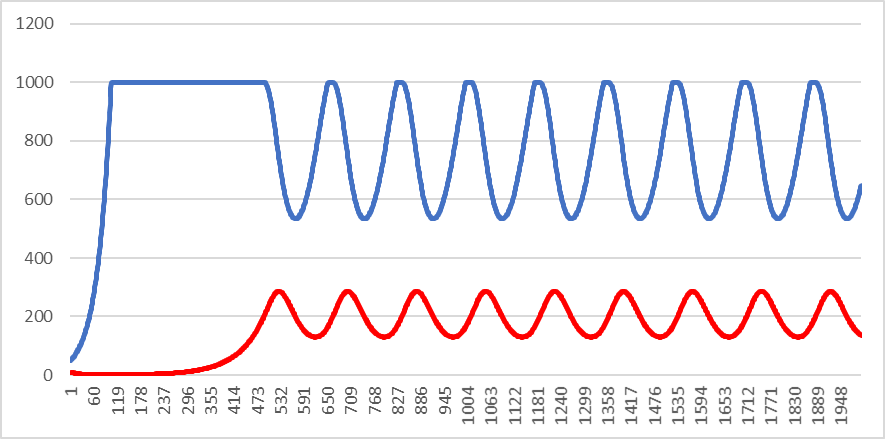
در شبیهسازی بالا، جمعیت روباهها و خرگوشها از طریق فرمولهای زیر محاسبه میشود. دلیل سقف جمعیتی ۱۰۰۰ برای خرگوشها، محدودیت منابع آنهاست. فرض مدل این است که در صورت ازدیاد جمعیت خرگوشها، زادولد برای آنها غیرممکن میشود.
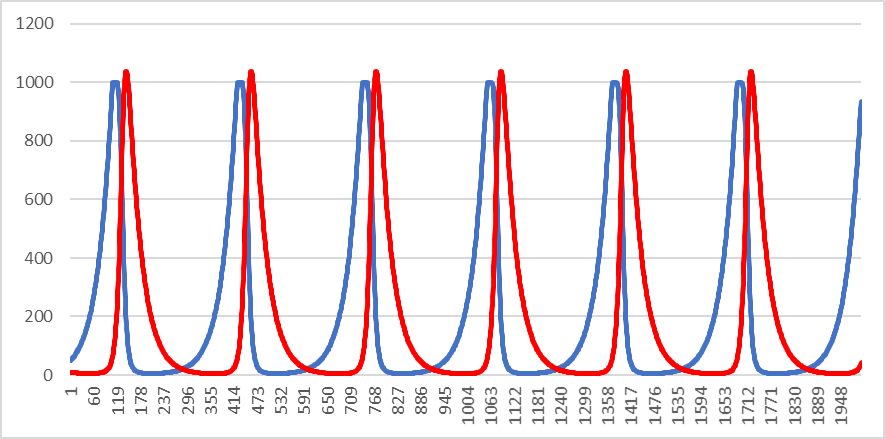
=MIN(MAX(B2+(($E$2*B2)-($F$2*B2*C2))*$G$2,0),1000)=MAX(C2+(($E$5*C2*B2)-(C2*$F$5))*$G$2,0)علاوه بر پیشبینی آینده، با بالا و پایین کردن متغیرها هم میتوان تأثیر هرکدام را بر روی خروجیها سنجید. مثلاً نمودارهای زیر اثرات متغیرهای fb و fd را بر روی جمعیت روباهها و خرگوشها نشان میدهد.
 |
|---|
 |
|---|
در صورت داشتن فرمولهای مدل دینامیکی، شبیهسازی در محیطهای مختلف ممکن میشود. مثلاً سایت زیر نمونهٔ شبیهسازی با کمک زبان javascript است3.
ضعف مدلهای دینامیکی در پیشبینی
مدلهای دینامیکی با همهٔ زیباییهایی که دارند، در پیشبینیهای واقعی بسیار ضعیف عمل میکنند. علت عملکرد ضعیف آنها، روابط غیرخطی موجود در دنیای واقعی است. پیچیدگی برخاسته از این روابط، کاری میکند که با دستکاری متغیرها در مقیاس هزارم و دههزارم، خروجی به کلی عوض شود. یک مثال ساده از این پیچیدگی، شبیهسازی آونگ دوتایی است که در آن با تغییر جزئی یک آونگ دوتایی نسبت به دیگری، بعد از مدتی حالت آنها به کلی با هم تفاوت پیدا میکند.
پیشبینیهای برخاسته از مدلهای دینامیکی هم همین حال را تجربه میکنند؛ به دلیل وابستگی شدیدی که به مقدار متغیرها دارند، هیچ حالتی را برای تصمیمگیر حذف نمیکنند. قوت مدلهای دینامیکی در ردهٔ انتزاع و مدل ذهنی است. به نظر من، آوردهٔ اصلی تفکر سیستمی معرفی مفهوم روابط غیرخطی و تئوریزه کردن آن بود.